Interpretability

Reading Dario Amodei's Blog Post The Urgency of Interpretability was pretty interesting, because in the sense of classic ML such as decision tree's, regression, and K-Means clustering, we're able to actually trace input to output with levels of interpretability as to "why the output was what it was". Cristophm Interpretability Blog discusses interpretability in depth, and both led to this blog post.

Dario's blog post highlighted the need for this in LLM's, and from a more granular level in deep learning networks with hundreds of thousands of nodes - there's a typical viewpoint of hierarchical features where, for example in a vision network, base layers represent horizontal and vertical lines, the next layers represent circles, triangles, and shapes, and then down the line the model can learn real world objects by combining lower level features. This hierarchical viewpoint is one of the more "appreciated" frameworks. Much work has gone into Mechanistic Interpretability to open up these black boxes, and it's made up of ideas like Circuits, Sparse Autoencoders, and other features. These are apart of Anthropic's interprtability framework Garcon

Interpretability is different from accuracy - a model can be accurate without being interpretable, and vice versa, and accuracy will come via model metrics on some sort of validation dataset. Interpretability is hard to score, regression is interpretable, but it's around averages of weights over the input, whereas decision tree's can sometimes come with exact rules that showcase the route a model takes to output. Both showcase what things weigh on input, but there's no exact metric / score for interpretability. Interpretability looks to answer "why did the model output this"

There is a difference between Classic ML Interpretability and Deep Learning (and LLM) Interpretability - Classical ML is usually more interpretable, whereas Deep Learning hasn't found a robust framework across large neural nets.

Typical Methods (mostly in Classical ML):

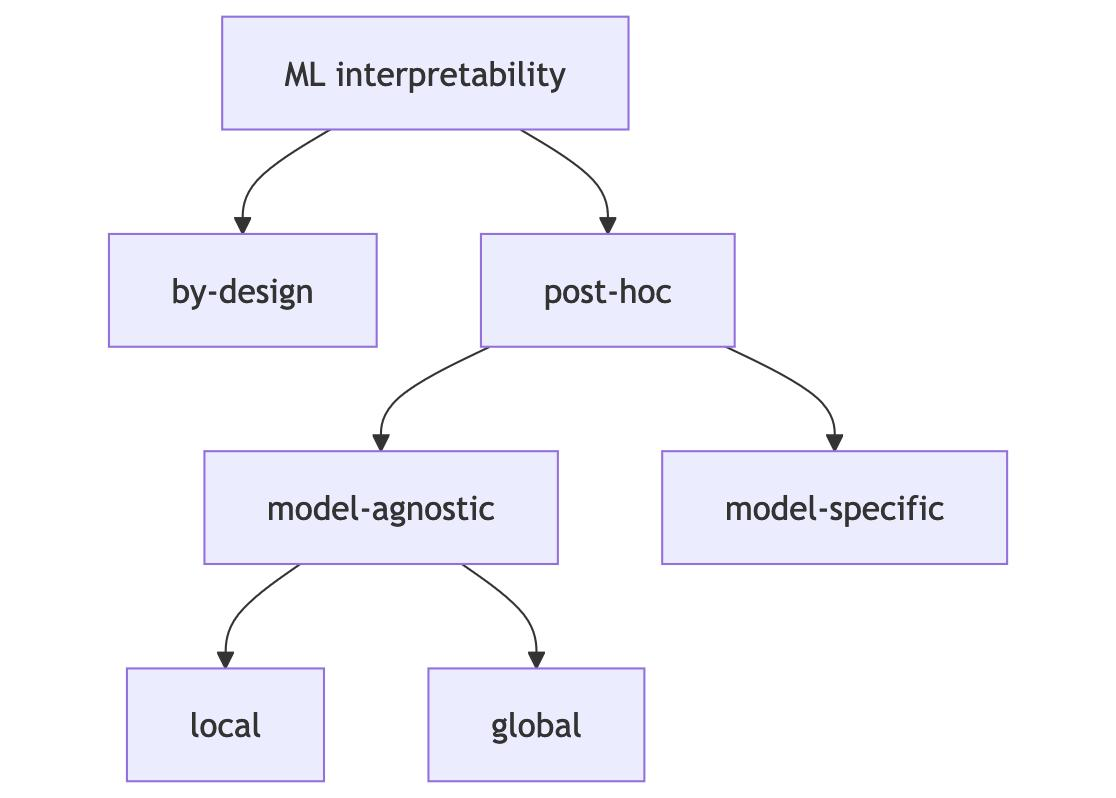
Interpretable by design: Means you train inherently interpretable models such as decision tree's
Post-hoc interpretable: Means using a specific interpretability method post training1
- Model agnostic do not depend on input model
  - Model agnostic methods follow the SIPA principle:
    - Sample from the data
    - Perform an intervention on it
    - Get predictions for manipulated data
    - Aggregate the results
  - Permutation feature importance is one example which measures the drop in model score after a model feature's values are randomly shuffled
    - Take a data sample
    - Permute it / shuffle around values of specific features
    - Get model predictions
    - Compute model error again and compare to original loss (aggregation)
- Model specific are typically per model
  - Analyzing features of a neural net is an example here
  - Local methods help to focus on single points, and help debugging by "zooming in" to view how the model is interacting with a data point, and global methods are useful in debugging an entire model on how it interacts with features of data
  - Local methods focus on explaining individual predictions
    - Some types:
      - Ceteris Paribus plots show how changing a feature changes a prediction
      - Individual conditional expectation curves show how changing one features changes the prediction of multiple data points
      - Local surrogate models explain a prediction by replacing the complex model with a locally interpretable one
      - Scoped rules are rules that describe which features values "anchor" a prediction
      - Shapley values fairly assign the prediction to it's individual features
      - SHAP is a computation method for Shapley values, but also suggests global interpretation methods based on combinations of Shapley values across the data
    - SHAP + Shapley values are attribution methods that explain a data points predictions as a sum of feature effects, and ceteris paribus and ICE focus on individual features
  - Global methods focus on entire datasets and batches over multiple predictions on average
    - Some types:
      - Accumulated local effect plots is a feature effect method
      - H-Statistic feature interaction quantifies the extent to which the prediction is a result of joint effects of the features
      - Functional decomposition is a central idea of interpretability and a technique for decomposing prediction functions into smaller parts
      - Permutation feature importance measures the importance of a feature as an increase in loss when feature is permuted
      - Leave one feature out removes a feature and measures increase in loss after retraining model without it
      - Surrogate models replace the original model with a simpler one for interpretation
    - It's clear to see a majority of these focus on features, and the effects of loss and accuracy after tweaking features
      - This means it requires large validation datasets, and clear features
      - Feature effects are about showing the relationship between inputs and outputs
      - Feature importance is about ranking the features by importance, where importance is defined by each method
    - These all typically help to show stakeholders the most important features, but they can't explain "why this row came out this way"

Classic ML

Linear Regression Interpretability
- Linear regression is typically very easy to interpret, and all of it's weights have easy to interpret meanings, along with measurements around confidence and feature importance baked into the model
Logistic Regression Interpretability focuses on how log odds are updated
- The interpretation is similar to Linear Regression, except a one unit update of a weight corresponds to an increase / decrease in log odds output
[GLM and GAM Interpretability]

Neural Networks

Neural networks involve millions of multiplications on weights, linear and non-linear transformations, and multiple parallel architecture components inside of it

Outside of that, there's a typical viewpoint of hierarchical features where, for example in a vision network, base layers represent horizontal and vertical lines, the next layers represent circles, triangles, and shapes, and then down the line the model can learn real world objects by combining lower level features.

Some typical neural network techniques:

Learned Features: What features did the neural network learn?
Saliency Maps: How did each pixel contribute to a particular prediction?
Concepts: Which concepts did the neural network learn?
Adversarial Examples: How can you fool the neural network?
Influential Instances: How influential was a training data point for a given prediction?