Pregel

Pregel, and Pregel based SDK's like Spark Graph-X, are used for traversing graphs using super-steps and message passing

Pregel Lecture Paper is another good discussion point that shows how pregel is setup and used on Spark, and some of the actual implementations for Basic Linear Algebra Support (BLAS) operations

Why It's Needed

The main reason I've used this in the past is that our Data Warehouse wrote things to Parquet or Delta format on Disk, and so our entire data model that was graph based had no actual way of traversing

Spark doesn't have recursion built in, and so a lot of groups ended up trying to write each "step" to disk and read it in to mimic recursion

input --> transform --> output1
write output1 to disk
output1 --> transform --> output2
...

And that means they were constrained to how many "outward hops" they could search if you view this from a Breadth First Search

Looking at the below DAG Example, if you start at Node 1, you can reach Node 5 in:

3 hops: $1 \rarr 3 \rarr 2 \rarr 5$
4 hops: $4 \rarr 1 \rarr 3 \rarr 2 \rarr 5$

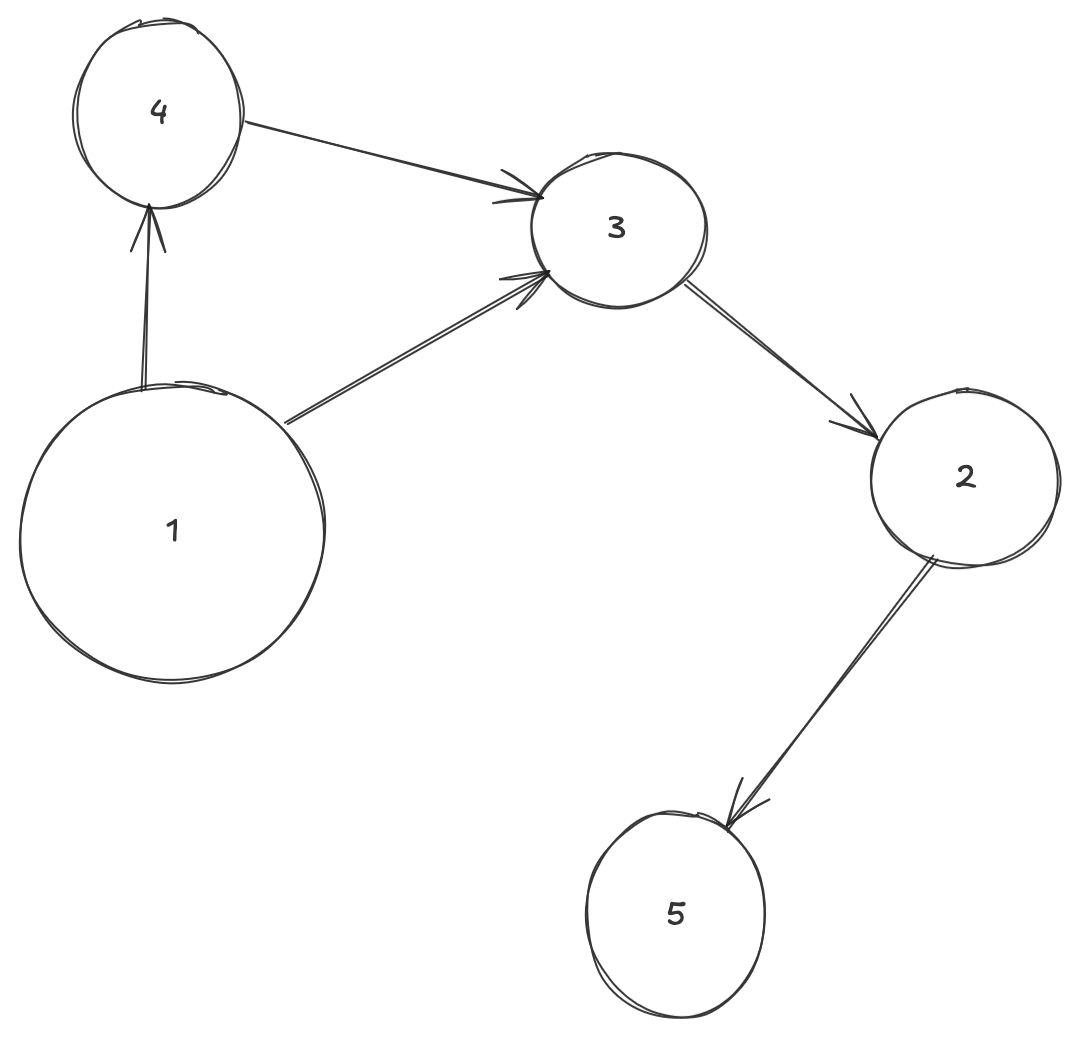
Dag Example

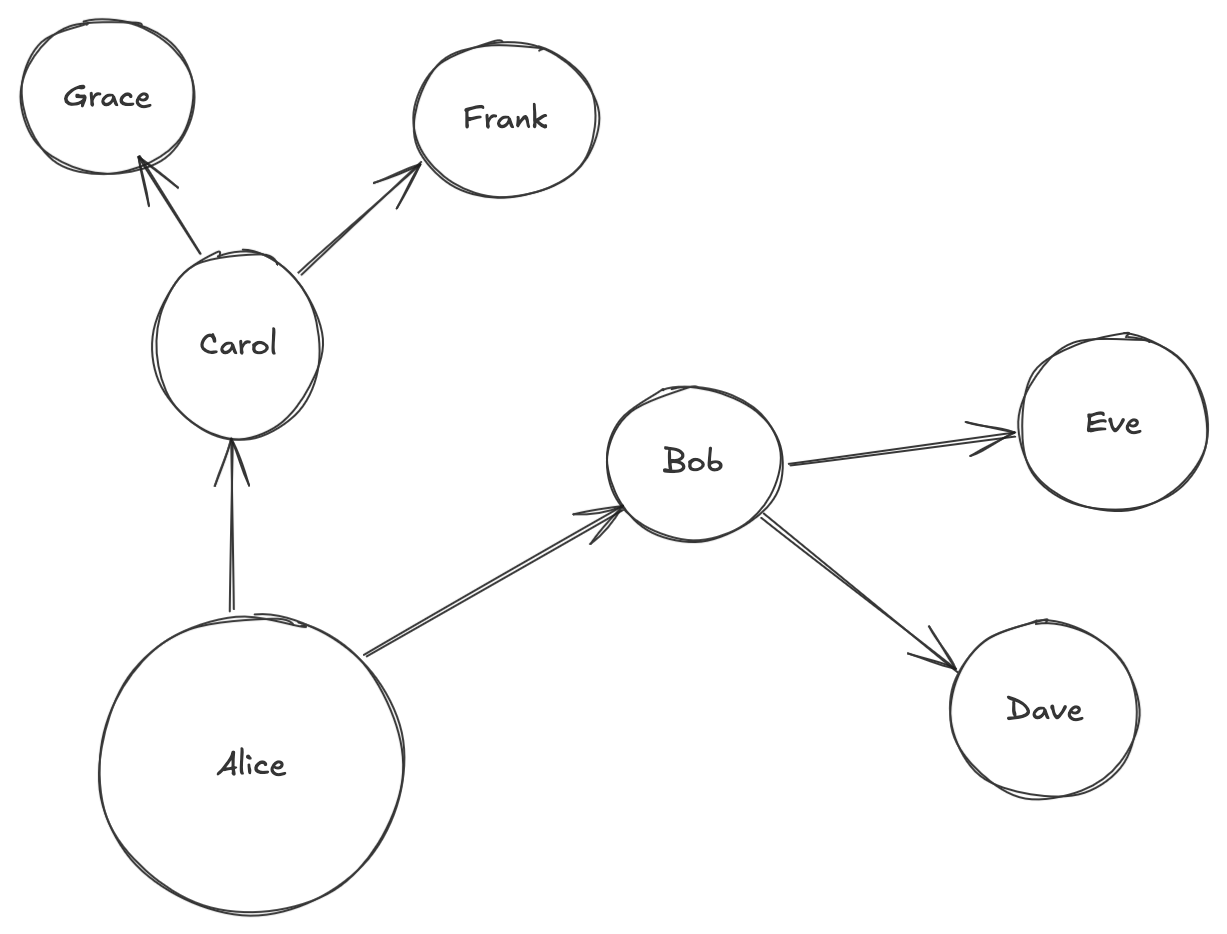
This works fine if you have a hierarchy:

Boss	Employee
Alice	Bob
Alice	Carol
Bob	Dave
Bob	Eve
Carol	Frank
Carol	Grace

Because at that point you can just find the max number of hops (in this case 2) and traverse that many times - it's not efficient, but it'll cover the entire graph

Hierarchy

It will fail if there are loops! Similar to social networks, corporate ownership structures, and many other phenomena

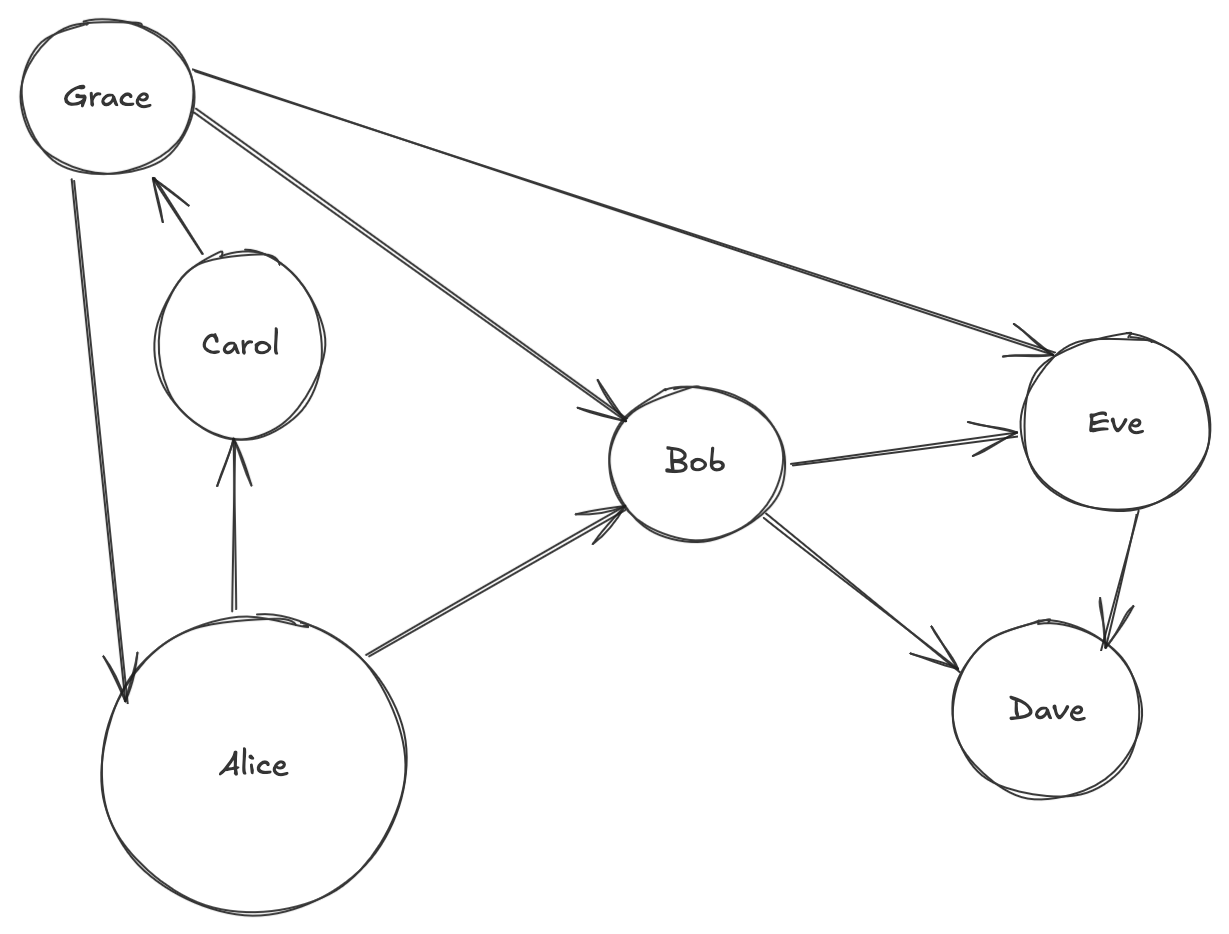
Loops

Even if you set n to something large, it'll continue to loop around and around

To solve a number of these issues you look to Pregel

How I See It

Really the most intuitive way to view the super-steps and message passing is in the lens of Breadth First Search

The pseudocode for BFS is:

q = queue([start_node])

while q:
    curr_step_size = len(q)
    for _ in curr_step_size:
        curr_node = q.pop()
        for neighbor in graph[curr_node]:
            q.push(neighbor)
            do_some_edge_logic
        
        do_some_curr_node_logic
    
    do_some_step_logic

Let's start with Alice in below example:

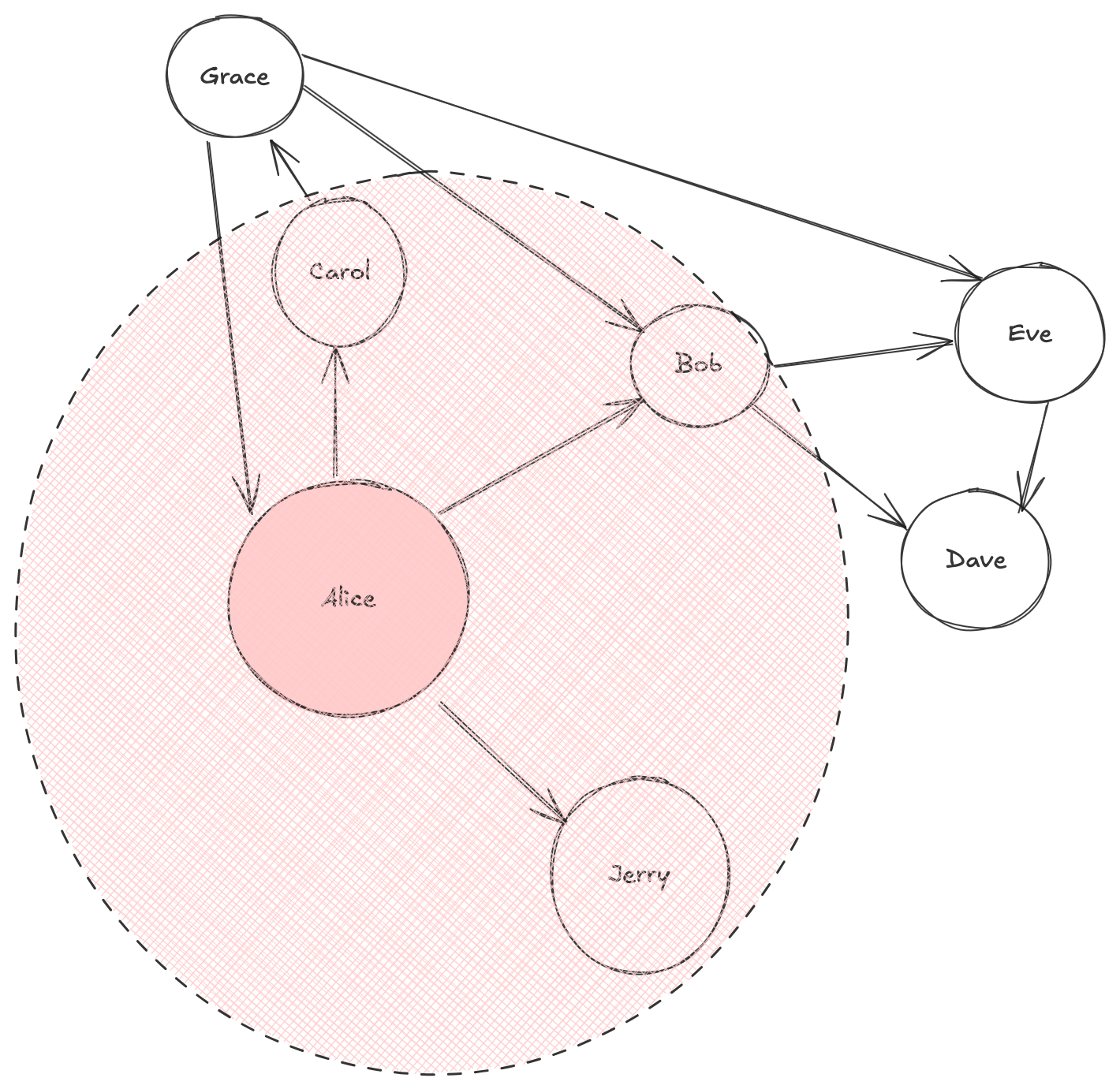
Below shows all of the neighbor we'd see in the first step, and this would equate to one "pulse" out from Alice Alice Step1

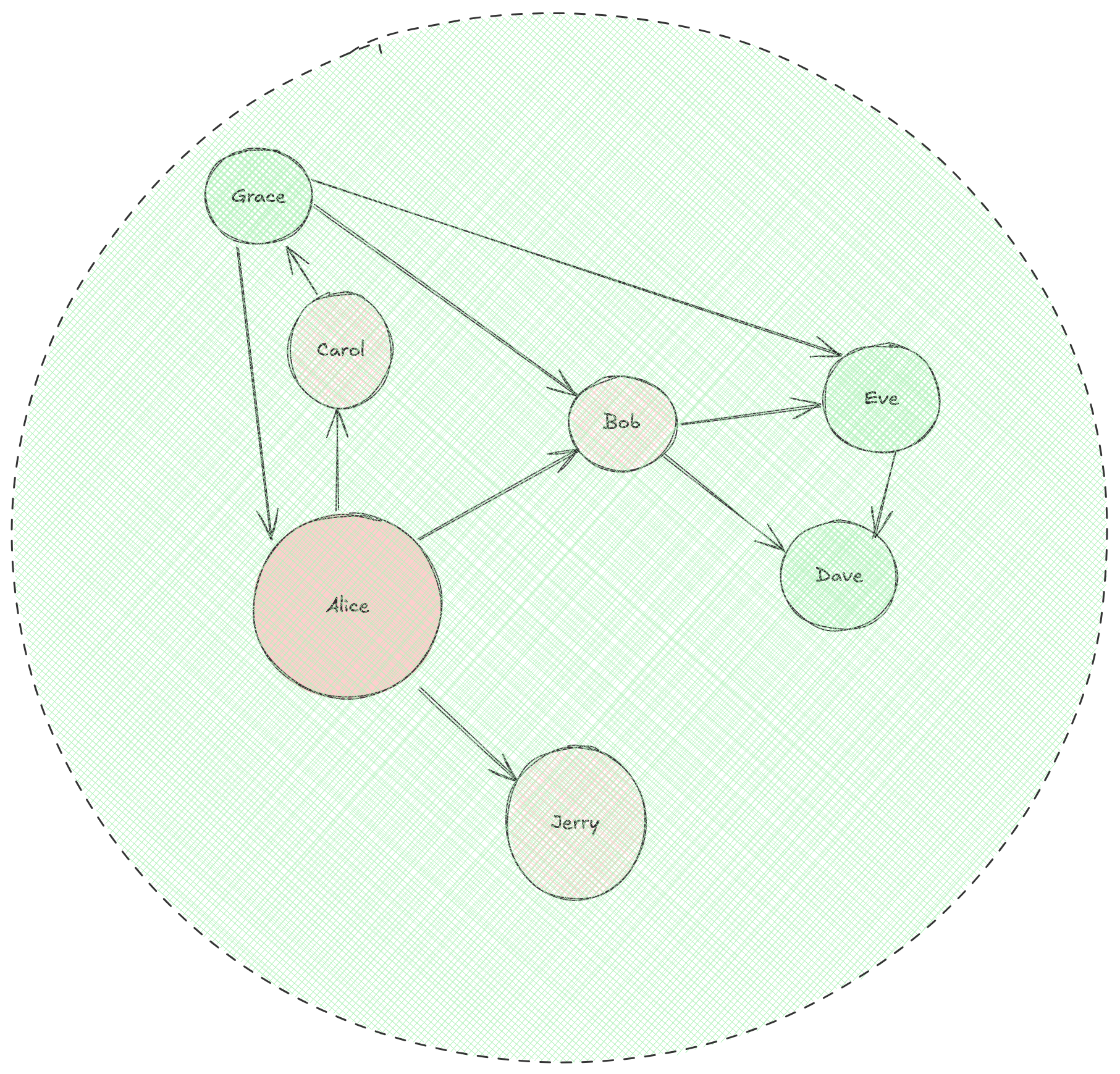
In the next step out we'd encompass all remaining nodes Alice Step2

However, you wouldn't have encompassed all remaining edges - the edge from Grace --> Alice was 3 hops away

Oh well, this shows how each "step" or "hop" moves outwards from the central node you're looking at

Pregel Implementation

Pregel Vocabulary:

Vertex: This is a Node / item in the Graph
- Most Vertexes will have Attributes or metadata that describe it
Edge: This is a link between 2 Vertexes, sometimes it has it's own information such as weight
Message: In each Super-Step, you would send out Messages along the Edges to our Neighbor Vertexes
- In the pseudo-code, it'd be do_some_edge_logic
Vertex Program: AKA vProg, is the actual transformation logic ran when you discuss do_some_edge_logic - it is defined as a function
Super-Step: you explained this above, and it's basically a "pulse" out from any Vertex - it's one more level out in a Breadth First Search paradigm
- The Super-Step Loop is one iteration of the loop, and it will run until no messages are sent
  - There's a chance that our Graph is a LinkedList, and it will just run $O(V)$ loops

The signature of Pregel itself in Spark showcases this:

def pregel[A]
      (initialMsg: A,
       maxIter: Int = Int.MaxValue,
       activeDir: EdgeDirection = EdgeDirection.Out)
      (vprog: (VertexId, VD, A) => VD,
       sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
       mergeMsg: (A, A) => A)
    : Graph[VD, ED]

The function is a generic type A which showcases the kind of message that's being sent between all nodes - usually this is just a case class
initialMsg holds the initial message that should be sent to every node on start
maxIter is an upper bound on number of iterations to run. It's mostly a stop gap from infinite looping
activeDirection direction not directory controls whether messages are sent via outbound or inbound direction of an edge
- The most common is outbound - at any node you store and process some state, and send the results outwards to all neighbors
vprog itself is a function compromised of
- vertexId which is just an identifier
- VD vertex data, which stores state of that node
- A which is a sent message of generic type A
- vprog stands for Vertex Program, and it's essentially the process that runs on each node internally before sending data outwards
sendMsg will take an edge triplet and returns an array of tuples composed of a vertex ID and a message
- This is the function used to generate messages to send outwards in the next super step of the iteration loop
mergeMsg would then run on each receiving node that would accept one or many sendMsg, and they would update their internal VD vertex state based on the aggregation of messages
- count, min, max, etc
It returns another Graph[VD, ED] which is a graph of the same type of vertex and edge data, but the vertexes are (hopefully) a mutated version of the input

Therefore, Pregel's implementation can intuitively be viewed as running Breadth First Search across all nodes in a distributed compute environment!

Let's say you have a Spark cluster with 5 nodes:

1 driver and 4 workers
The 4 workers have 4 cores each
So you have 16 cores total to process data with
At the beginning each node would get it's initialMsg and would sit on a core, and then we'd simply start running BFS for each node
- Any node can receive many inputs, and they'd need to merge all of these in-edges, run some logic, and then send a message outwards
Initial Message: Start off each Vertex with some initial message / starting point
- Most of the time the initial message is some attribute like "Name", "Role", or "Salary"
Send Message: As you move out from any single Vertex to any other Vertex in a "hop", you send a message to it with some information
- This can be based on infromation we've gotten in previous hops, or solely based on that Vertex's own information
- In the example above:
  - Bob receives messages from Grace and Alice
  - Bob sends messages to Eve and Dave
Merge Message: Any Vertex can receive multiple incoming messages, and when that happens some logic needs to be ran on all of them
- map: x -> x+1 would add 1 to every element:
  - [1, 2, 3] --> [2, 3, 4]
- flatMap: x -> sum() would aggregate everything:
  - [1, 2, 3] --> 6
- Tons of other functional programming functions are also available - MAX, MIN, AVG, MODE
  - you can merge this as any sort of data type, be it Int, Array, Struct, etc...

Psuedo-code:

for vertex in vs:
    vertex.msg = initialMsg

while some_msg_sent:
    for v_with_msg in vs_with_msgs:
        msgs = []
        for msg in incoming_msgs:
            msgs.append(msg)
        
        curr_msg = mergeMsg(msgs)
        sendMsg(curr_msg)
    
    n_iterations += 1

return(result)

Throughout the examples below, you'll see new definitions for mergeMsg, sendMsg, and initialMsg for each different algorithm

So at this point you see how Vertexes are held, how you pass messages (traverse), how logic can be ran, and how this all avoids recursion + writing to disk in-between!

Common Examples

Common examples include Max Propogation, Single Source Shortest Path, Page Rank, and Transitive Closure

Max Propogation

Max propogation is just that you want our max value "carried" around to all weights - so if there's a 100 in a sea of 1's, after the program terminates all of the Vertices will know the global maximum is 100

val graph = Graph(vertices, edges)

val initialMsg = 0

def vprog(id: VertexId, attr: Int, msg: Int): Int = math.max(attr, msg)

def sendMsg(triplet: EdgeTriplet[Int, Int]): Iterator[(VertexId, Int)] = {
  // if our current source node has a higher value than destination, send message to destination
  if (triplet.srcAttr > triplet.dstAttr)
    Iterator((triplet.dstId, triplet.srcAttr))
  else
    Iterator.empty
}

// if you receive multiple incoming messages, just take max one and then check if you should forward
def mergeMsg(a: Int, b: Int): Int = math.max(a, b)

val result = Pregel(graph, initialMsg)(vprog, sendMsg, mergeMsg)

Single Source Shortest Path (Djikstra)

In normal day-to-day folks use Djikstras Algorithm for finding the shortest path between a single Vertex and all other Vertices, here you show how to do it in Pregel over a large graph

The Single Source Shortest Path is when you need to find the shortest path from a source Vertex $v$ to all other Vertices in the graph

Single Source Shortest Path

import org.apache.spark.graphx.{Graph, VertexId}
import org.apache.spark.graphx.util.GraphGenerators

// A graph with edge attributes containing distances
val graph: Graph[Long, Double] =
  GraphGenerators.logNormalGraph(sc, numVertices = 100).mapEdges(e => e.attr.toDouble)
val sourceId: VertexId = 42 // The ultimate source


// Initialize the graph such that all vertices except the root have distance infinity.
val initialGraph = graph.mapVertices((id, _) =>
    if (id == sourceId) 0.0 else Double.PositiveInfinity)
val sssp = initialGraph.pregel(Double.PositiveInfinity)(
  (id, dist, newDist) => math.min(dist, newDist), // Vertex Program
  triplet => {  // Send Message
    // If current node srcAttr sent to it plus it's own distance is less
    //  than a neighbors total length, send over it's info 
    if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {
      Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))
    } else {
      Iterator.empty
    }
  },
  (a, b) => math.min(a, b) // Merge Message
)
println(sssp.vertices.collect().mkString("\n"))

PositiveInfinity portion is the initial message sent to all nodes
the val sssp is the actual entire program, which just checks if the message received, newDist, is smaller than the current assigned shortest distance dist
- If this is true the VD data is updated with this information instead of the historic info
- All nodes start with VD of inf, so most get updated in the first pass of data over them
The triplet => lines have the actual logic for sending messages outwards to other nodes
- srcAttr is the current node's seen distance
- attr is the edge distance between src --> dst
- dstAttr is the receiving node's seen distance
- vProg sends a message to a receiving node if the current node + edge distance is less than the receiving nodes distance - i.e. if there's a chance to find a lower path
  - The receiving node will then aggregate all incoming messages and merge them via (a, b) => math.min(a, b)
  - This means for it's state a, and any incoming message b, pick the min - this will result in choosing the min over all incoming messages which will be the shortest path overall incoming
Each node is constantly checking and updating it's state if it's received a message, and only sending out messages if it's state has changed and the relevant sendMsg logic is covered
Once no more messages, or maxIter is reached, the program will stop, and we can find the shortest total distance from sourceId to any other node if we simply query the VD vertex data of that node

Note this is one pass for a single source node, and so if we want to find the shortest path from any node to any other node, we'd need to pre-compute this, store it, and then re-run this algorithm if any edge distance changes in the future

Page Rank

Page Rank is basically the Hello World of graph processing and traversal - it was used in Google in the beginning to rank Vertexes, where the more important the Vertex the higher the Rank

It used webpage links + relative importance to decide other webpage importance - if you have 100 very important websites pointing to you, you're probably important

Formula: $PR(v) = (1 - d) + d \cdot \sum_{u \in N - (v)} {PR(u) \over deg(u)}$

Parameters:
- $d$ is the dampening coefficient which helps us to weight incoming links
- $u \in N - (v)$ are all of the links coming in that aren't from the Vertex itself
- $\sum_{u \in N - (v)}$ $\sum_{u \in N - (v)}$ is the aggregation of all of the links coming in
  - $PR(u)$ is rank of an incoming link
  - $deg(u)$ $d e g (u)$ is the in-degree, meaning you give lower scores to webpages who spray out links everywhere
    - If there are 800 links on a page, it's probably not a good reference page
    - If there's 2 links, and it's a highly ranked page, the $PR(u)$ won't be reduced by much (1/2)

val links: RDD[Edge[Int]] = sc.parallelize(Seq(
  Edge(1L, 2L, 1), Edge(1L, 3L, 1),
  Edge(2L, 3L, 1),
  Edge(3L, 1L, 1)
))

val graph = Graph.fromEdges(links, 1.0).mapVertices((_, _) => 1.0)

val numIter = 10
val damp = 0.85

val outDegrees = graph.outDegrees
val graphWithDegrees = graph.outerJoinVertices(outDegrees) {
  (vid, rank, degOpt) => degOpt.getOrElse(0)
}

val prGraph = graphWithDegrees.mapTriplets(triplet =>
  1.0 / triplet.srcAttr
)

val initialMessage = 0.0

def vprog(id: VertexId, attr: Double, msgSum: Double): Double = {
  (1 - damp) + damp * msgSum
}

def sendMsg(triplet: EdgeTriplet[Double, Double]): Iterator[(VertexId, Double)] = {
  Iterator((triplet.dstId, triplet.srcAttr * triplet.attr))
}

def mergeMsg(a: Double, b: Double): Double = a + b

val result = Pregel(prGraph.mapVertices((_, _) => 1.0), initialMessage, numIter)(
  vprog, sendMsg, mergeMsg
)

result.vertices.collect.foreach { case (id, rank) =>
  println(s"Vertex $id has rank: $rank")
}

Connected Components

This is a very important algorithm that will find you the clusters of Vertexes in a graph - if every Vertex is connceted, the number of components is 1

Usually you'll find a number of "islands" and each island is a connected component

In connected components you must "drag along" the minimum ID as it's the best identifier, the max would work as well - you need something that you can reference as the min

It's equivalent to the Max Propogation algorithm, with a slightly different sendMsg

import org.apache.spark.graphx._

// Sample undirected graph
val edges: RDD[Edge[Int]] = sc.parallelize(Seq(
  Edge(1L, 2L, 1), Edge(2L, 3L, 1),
  Edge(4L, 5L, 1), Edge(5L, 6L, 1)
))

val graph = Graph.fromEdges(edges, defaultValue = Long.MaxValue)
  .mapVertices((id, _) => id) // Initialize each vertex with its own ID

// Vertex Program: keep the smallest ID seen
def vprog(id: VertexId, attr: VertexId, msg: VertexId): VertexId =
  math.min(attr, msg)

// Send the current value to all neighbors
def sendMsg(triplet: EdgeTriplet[VertexId, Int]): Iterator[(VertexId, VertexId)] = {
  // srcAttr is current componentId of srcVertex, dstId is neighbor
  //    in this example you will send src componentId to dstId, and send dst componentId to srcId
  // If this were directed, you could remove one of these
  Iterator((triplet.dstId, triplet.srcAttr), (triplet.srcId, triplet.dstAttr))
}

// Merge messages: pick the smallest
def mergeMsg(a: VertexId, b: VertexId): VertexId =
  math.min(a, b)

// Run Pregel until convergence
val cc = Pregel(graph, initialMsg = Long.MaxValue)(
  vprog, sendMsg, mergeMsg
)

cc.vertices.collect.foreach { case (id, comp) =>
  println(s"Vertex $id belongs to component $comp")
}

Transitive Closure

Lastly is transitive closure - this relates to a reachability set of a node

For every Vertex $u$ , find all other Vertices $v \in V$ such that there's a path from $u \rarr v$

you represent the state of each vertex as a set of reachable ID's

This can absolutely blow up memory, and is most useful when bounded to $k$ steps

val edges: RDD[Edge[Unit]] = sc.parallelize(Seq(
  Edge(1L, 2L, ()), Edge(2L, 3L, ()),
  Edge(3L, 4L, ()), Edge(1L, 5L, ())
))

val graph = Graph.fromEdges(edges, defaultValue = Set.empty[VertexId])
  .mapVertices((id, _) => Set(id)) // each vertex starts with itself

def vprog(id: VertexId, attr: Set[VertexId], msg: Set[VertexId]): Set[VertexId] =
  attr ++ msg

def sendMsg(triplet: EdgeTriplet[Set[VertexId], Unit]): Iterator[(VertexId, Set[VertexId])] = {
  // if dstAttr is not a proper subset of our seen vertices, send our set to destination
  //    I believe if our set is (1, 2, 3) and dst is (1, 2, 4) you will still send our entire set
  if (!triplet.dstAttr.subsetOf(triplet.srcAttr)) {
    Iterator((triplet.dstId, triplet.srcAttr))
  } else Iterator.empty
}

// add any other vertices to our attribute, ensure it's a set
def mergeMsg(a: Set[VertexId], b: Set[VertexId]): Set[VertexId] =
  a ++ b

val closure = Pregel(graph, initialMsg = Set.empty[VertexId], activeDirection = EdgeDirection.Out)(
  vprog, sendMsg, mergeMsg
)

closure.vertices.collect.foreach { case (id, reachable) =>
  println(s"Vertex $id can reach: ${reachable.toList.sorted.mkString(", ")}")
}

Pregel​

Why It's Needed​

How I See It​

Pregel Implementation​

Common Examples​

Max Propogation​

Single Source Shortest Path (Djikstra)​

Page Rank​

Connected Components​

Transitive Closure​