Table of Contents

Candidate Generation

The reason candidate generation is so useful, is because it typically allows us to reduce our search space from the entire corpus, typically petabytes in size, to a searchable susbscape of typically hundreds or thousands of items

It’s also done relatively quickly, ideally in a way where we can index / lookup a matrix or user history in a relatively fast fashion, on services that have been updated in the background by our web servers. Basically, we are hoping that as users use our service their item and user history have been being updated and sent to our search systems in real-time, and when we need this information our architecture is setup to be real-time responsive

In Candidate Generation, Queries are Users and we compare them to Items

User-Item Matrices

Our Embeddings concept paper discusses this in detail, but for all of our systems we generally have 2 key components - queries (users) and items

Over time users engage with items (which might be other users!), and this is a scorable numeric metric - they either rank them (movies), watch them (Youtube video watch time), read them (Newspaper post read through length), or engage with them (check another users page)

These co-occurrence matrices showcase how our users (queries) interact / are related to our Items

For all intents and purposes, the matrix defined of our users and how they engage with items is perfectly fine to use as our embeddings. In the below example, let’s say it’s users video watch time, user 1 engages with item 1 for 90 minutes [ M = \begin{pmatrix} 90 & 4 & \cdots & 20
18 & 66 & \cdots & 25
\vdots & \vdots & \ddots & \vdots
110 & 46 & \cdots & 38 \end{pmatrix} ] Or maybe we can make it percentage of video watched through (it would be some numeric feature standardization) which would bring each number into the standardized range of $[0, 1]$ [ M = \begin{pmatrix} .9 & .2 & \cdots & .1
.35 & .5 & \cdots & .25
\vdots & \vdots & \ddots & \vdots
.05 & .99 & \cdots & .75 \end{pmatrix} ]

With this setup we have now projected our Users and Items into an Embedding Space $E \in \real^v$ where $v$ defines the total number of videos in our corpus. Since $v$ is probably humongous, we can use Matrix Factorization to decompose this into two separate matrices $U \in \real^{v’}, I \in \real^{v’}$ where $v’ \leq v$ to ultimately reduce the total size of our search space while preserving information

Similarity

If we want to find similar users, we have a search function $S: E \times E \rightarrow \real$ where $S(q, x)$ has a query $q$ and compares it to each other embedding $x$ in our embedding space to find similar vectors $x$, which may be Users or Items. This allows us some flexibility in “find similar users / items to user Q” and then we can use ScaNN (Scalable Nearest Neighbors) to find the Top K nearest vectors

Our Vector Similarity Scoring can be anything from Cosine to Dot products, but for this example if we normalize all of the vectors down to $[0, 1]$ we should be able to use either.

In any other example, a popular video tends to coincide with larger norms, and so our recommendation would probably favor those videos with the Dot product

Filtering and Factorization

Filtering leverages the idea that users who have agreed in the past will agree in the future, based on user similarity or item similarity

In either way we can use embedding matrices for Queries (Users) $U$ or Items $I$, or a combination of them. Similarity between items is calculated using metrics such as cosine similarity, Pearson correlation, or Jaccard index

To find recommendations, you compare the query (User embedding) to all Item embeddings using similarity metrics (e.g., dot product, cosine similarity), which will ultimately give you the top Items for a User

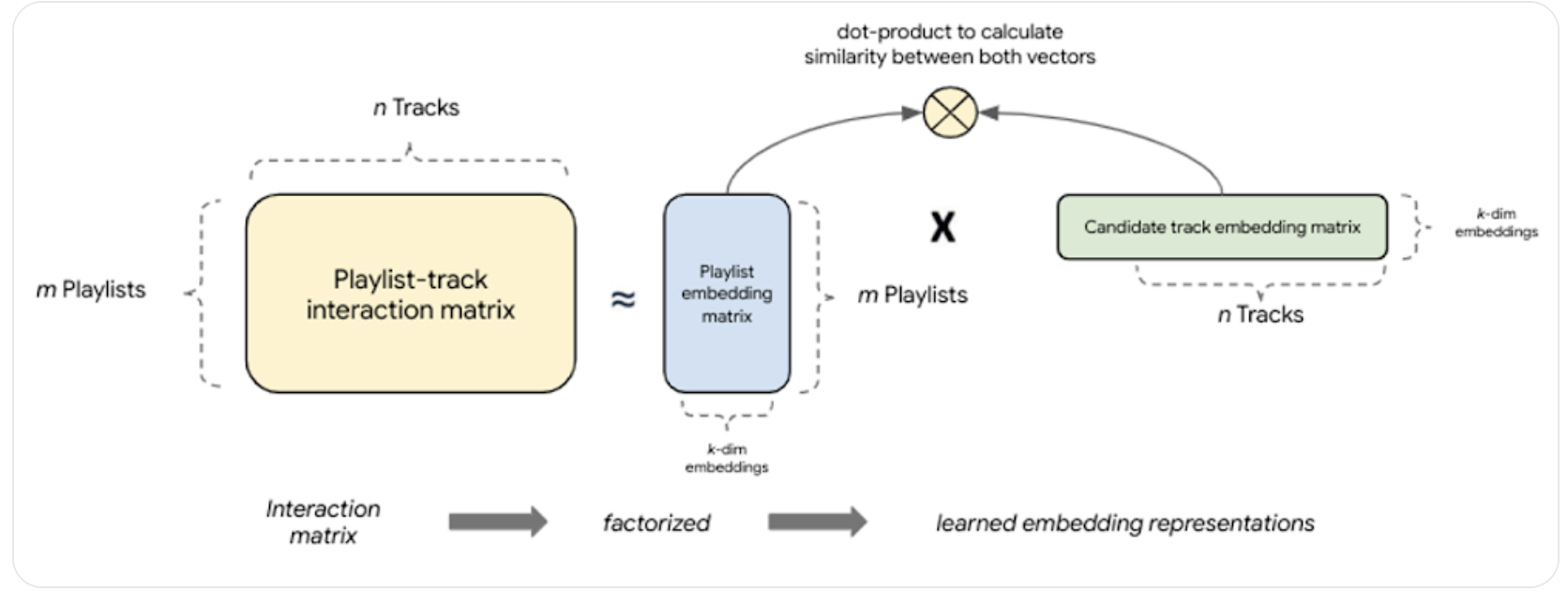
This example from Google shows how if we have $m$ Playlists who have $n$ songs we can use this co-occurrence matrix, factorize it, and then find similar Playlists. Factorizing these into $k$ dimensions allows us to find the Top-K Latent Features of each playlist, and ultimately to comapre it to other playlists using geometric vector distance. This is similar to facrotizing User x Item matrix, and then doing a dot product with $n$ items to find what ones would be useful to User. It’s a bit odd because we’re saying we can compare Track Embeddings to Playlist Embeddings, but ultimately we’re calculating the interaction score / goodness score of adding a new Track to a Playlist Google Songs

Item Content Filtering

Pros Cons
Don’t need user information for items  
Can compute quickly, and in a distributed manner Matrix has a large memory footprint

User-Item Collaborative Filteringit

Collaborative Filtering allows us to use Users and Items at the same time!. It recommends items to user A based on the preferences / history of similar user B

How Collaborative Filtering Works

Pros Cons
Able to introduce users to new items Cold start problem for new items
Clean interface / interaction Sparse datasets that take up a lot of memory
Can randomly seed user with user demographics Popular items get a disproportionate amount of attention

Collaborative Filtering Algorithm

Typically has a User-Item Matrix where Users are rows and Items are columns The below matrix is our embeddings, and as far as this page is concerned, that’s it!

[ M = \begin{pmatrix} r_{11} & r_{12} & \cdots & r_{1n}
r_{21} & r_{22} & \cdots & r_{2n}
\vdots & \vdots & \ddots & \vdots
r_{m1} & r_{m2} & \cdots & r_{mn} \end{pmatrix} ]

Where:

Some pseudocode for the actual algorithm to filter a specific user $U_i$, and find their $K$ nearest neighbors:

max_heap = heap()
for other_user in users:
    max_heap.push(
        struct(
            calculate_similarity(user_i, other_user),
            user_i,
            other_user
        )
    )

resp = []
for _ in range(k):
    resp.append(max_heap.pop())
return(resp)

function find_similar_users(user_item_matrix, target_user, K):
    # Step 1: Calculate similarity between target_user and all other users
    similarities = []
    for user in user_item_matrix:
        if user != target_user:
            similarity = calculate_similarity(user_item_matrix[target_user], user_item_matrix[user])
            similarities.append((user, similarity))
    
    # Step 2: Sort users by similarity in descending order
    similarities.sort(key=lambda x: x[1], reverse=True)
    
    # Step 3: Select the top K users with the highest similarity
    similar_users = [user for user, similarity in similarities[:K]]
    
    return similar_users

function calculate_similarity(user_vector1, user_vector2):
    dot_product = sum(a * b for a, b in zip(user_vector1, user_vector2))
    magnitude1 = sqrt(sum(a * a for a in user_vector1))
    magnitude2 = sqrt(sum(b * b for b in user_vector2))
    if magnitude1 == 0 or magnitude2 == 0:
        return 0
    return dot_product / (magnitude1 * magnitude2)

Matrix Factorization

Matrix factorization is a technique used in recommender systems to decompose a large matrix into smaller matrices. This technique is particularly useful for collaborative filtering, where the goal is to predict user preferences for items based on past interactions.

For the above discussion on Collaborative Filtering, we noticed one of the Cons was that this was a gigantic matrix and it’s difficult to actually run the collaborative filtering algorithm to find similar users…we need a way to get past this

Matrix factorization can help!

Explanation

  1. Decomposition:
    • Using the Matrix $M_{ui}$ from our discussion in collaborative filtering algorithm where the $U$ rows represent Users and the $I$ columns represent Items
    • Matrix factorization decomposes the original matrix into two lower-dimensional matrices:
      • User Matrix (U): $U_{ud}$ Represents latent features of users.
      • Item Matrix (V): $V_{id}$ Represents latent features of items.
      • Both of these matrices are based on the dimensions of $M_{ui}$ that get turned into $U_{ud}$ and $V_{id}$
    • The embeddings learned from decomposing $M$ gives us two new matrices, where the dot product $U_{ud} \cdot I_{id}^T$ gives us an approximation of $M$
      • To break this down, it means we can have 2 smaller matrices that we can pick and choose row / column pairs from to get the original matrix, which helps us to speed up queries and reduce memory footprint
    • The product of these two matrices approximates the original matrix.
  2. Latent Features:
    • Latent features capture underlying patterns in the data, such as user preferences and item characteristics.
    • These features are not directly observable but are inferred from the interaction data.
  3. Optimization:
    • The decomposition is typically achieved through optimization techniques that minimize the difference between the original matrix and the product of the two lower-dimensional matrices.
    • Common optimization methods include Singular Value Decomposition (SVD) and Alternating Least Squares (ALS).

Formula

Given a user-item interaction matrix ( R ), matrix factorization aims to find matrices ( U ) and ( V ) such that: [ R \approx U \cdot V^T ] Where:

First thoughts

Weighted Matrix Factorization

[ \min_{U, V} \left( \sum_{(i,j) \in \text{observed}} w_{ij} (r_{ij} - u_i \cdot v_j^T)^2 + w_0 \sum_{(i,j) \in \text{unobserved}} (u_i \cdot v_j^T)^2 \right) + \lambda \left( \sum_{i=1}^{m} |u_i|^2 + \sum_{j=1}^{n} |v_j|^2 \right) ]

Where:

Solving for this equation:

Pros Cons
No domain knowledge needed Cold start problem for new items
Battle tested and useful Not able to add in other side features
Good starting point for most rec systems for CG  

DNN For Candidate Generation

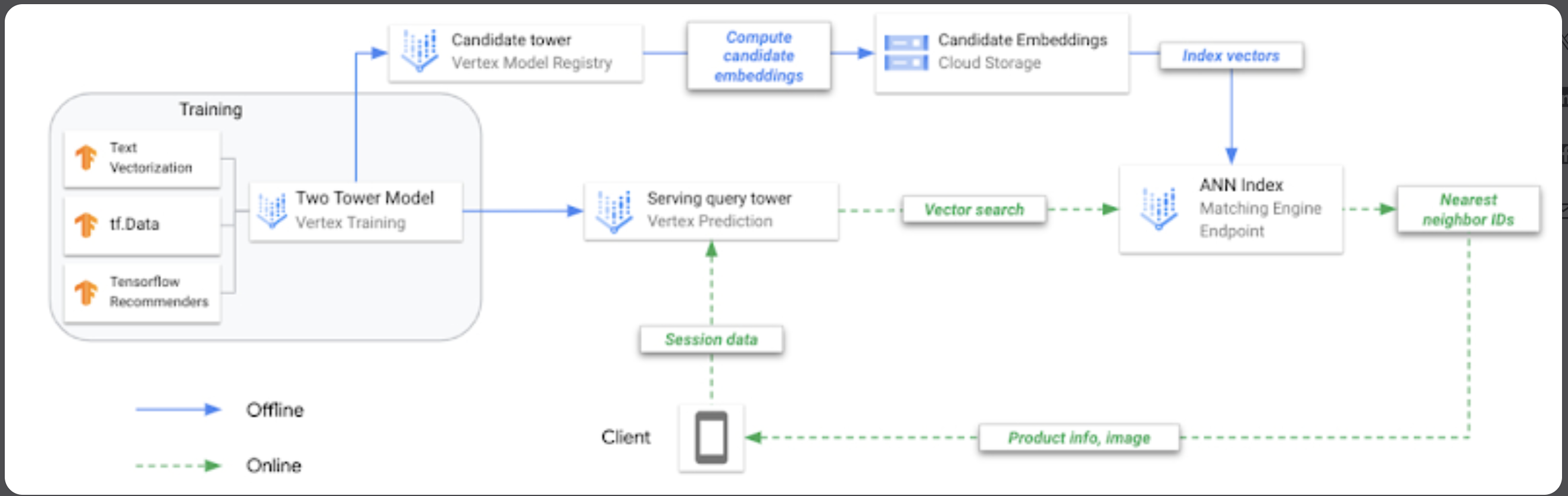
DNN allows us to reduce latency during serving time by decoupling Query Embedding and Item Embedding creation, but we are still using DNN instead of Matrix lookup so overall it might be slower. We can pre-compute Candidates (Items), and then store them in a Vector Type Database for quick lookup

Here’s an example of architecture from Google’s Blog Two Towers Example from Google

Two Towers

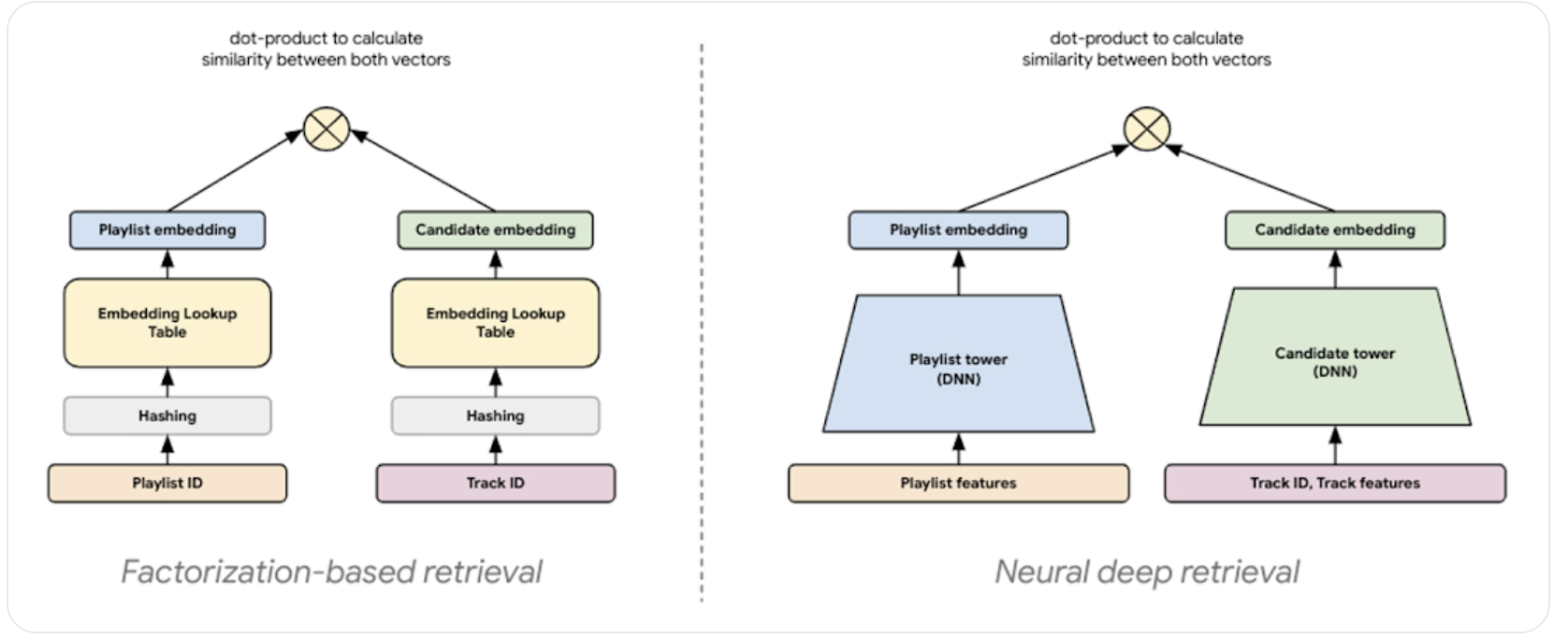
Two Towers will also generate embeddings for users and items, similar to Matrix Factorization, except in this scenario there’s one tower for Queries (Users), and one tower for Items. If we ran Two Towers for the same Factorization problem above about Playlist and Tracks it’d look like this TT Songs

The Two Towers will allow us to create Dynamic, and maybe even attended to embeddings, which is different from static embeddings created via Filtering & Matrix Factorization. At the end to get a recommendation it’s a similar option where we compute similarity of Query to all Items (maybe using ScaNN (Scalable Nearest Neighbors)) and find Top K

This will allow us to bypass the cold start problem, and the static embedding problem, but increases our latency as we need to use another DNN call in our Ranking service

Multi Tasks Learning

The tasks of this model are important, if we strictly focus on “probability of engaging” we might end up recommending click-bait videos, or if we do “time spent watching” it might recommend videos that try to get the user to keep watching long into the videos

Ultimately we want to use simple tasks to find relevant content for the users, and we could use multi-task learning to do so

TODO: Describe multi-task learning outputs and model weight updates using ./other_concepts/MULTITASK_LEARNING.md