6. Binary Search
Binary Search
lookup on sorted search space!
The entirety of binary search is around being able to find something in time because our data structure is sorted in some way - whether it's a Tree, a List, or a generic search space like the number line (rate of X, number of Y, etc... are just integers that are sorted)
At each step of the way you shrink the search space by half because you know the data structure is sorted in some way - if you were looking for a word in the dictionary that starts with D and you randomly flipped to the letters N, we'd look to the left
If you have some search space, lets say an array arr and there's an element x, then you can find the index idx of x in arr in time and space. Most of the time, searching via binary search is faster because it will beat out
Why is it ? Mostly because if there are elements, and you are constantly splitting it in half, then you'll do at most searches:
I guess that's just repeating the same thing twice - here's a photo:
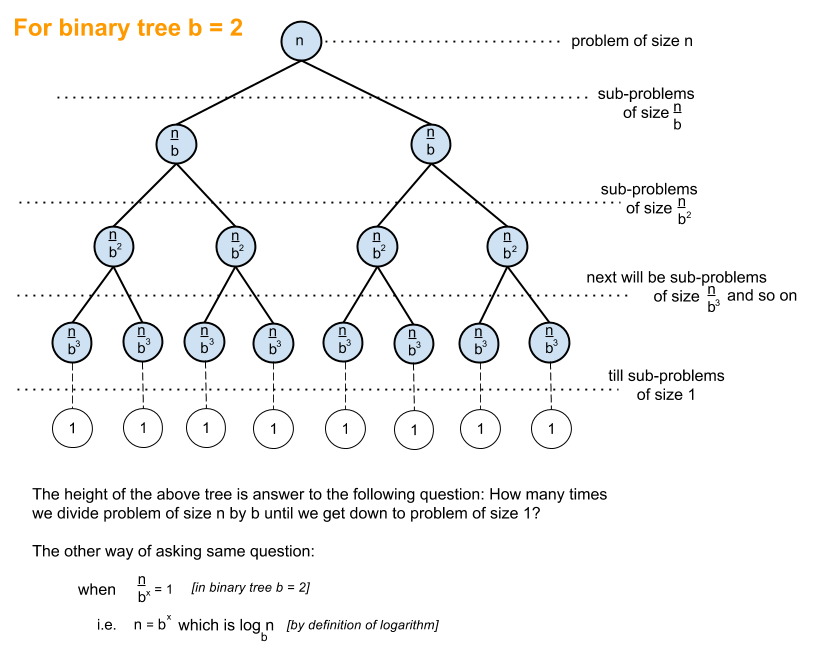
Intuition
If you have a sorted arr, and you have it's start and end indexes left, right you can continuously check the middle mid = left + right // 2, and based on mid relation to your target you can shrink the search space in half. If mid > target, that means you want to focus to the left and you'll change right = mid - 1, and if mid < target, that means you want to focus to the right and you'll change left = mid + 1
In Java or Cpp you'd use left + (right - left) / 2 so that, in case right = INT_MAX, you don't store something larger than it which would overflow
The template in Python pretty much does just that:
def binary_search(arr, target):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if check(mid, arr, target):
# do something
return
if arr[mid] > target:
right = mid - 1
else:
left = mid + 1
# target is not in arr, but left is at the insertion point
return left
def check(idx, arr, target):
return(
arr[idx] == target
)
Using len(arr) - 1 means your last valid index is included, and your valid search interval is [left, right]. In this you check left <= right
The main difference is what you return, and how you update your search space:
- If you want to return the exact index you can do that, or you can return an insertion point of where something new should be placed
- You can update your search space based on finding any match, the unique exact match, the first match of some kind, or the last match of some kind
Typical Problem Statements
Some will outright say "find this value in a sorted list" which makes things easy, most won't Other ways to describe it"
- Theres an array of times each train takes
- Array of times it takes to eat a meal
- Given a threshold k, what’s the minimum time each train / meal would take to finish
- Find an element in an array that's been sorted, and then rotated
- Capacity to ship packages within days (f' this one)
Most of these solutions will involve a check() function, where you will propose some item in the search space, like an index or other value, and then quickly check if that value works
For the capacity to ship packages problem, the check() function revolves around checking if the weight capacity can cover the shipping requirements - the check() funciton itself runs in time so it seems slow, but ultimately it's still fast compared to other routes
- In the above classic case,
check()is just comparing the element atarr[idx]totarget
The reason this is "fast" is that in time you can propose capacity values, and then for each of them it takes time to check so the overall solution is . This is faster than iterating from 1 to 2 to 3... capacity which would result in
Typical Patterns And Pitfalls
There are some typical patterns pitfalls that annoyingly come up in almost every review
The main questions to ask:
- What is the search space?
- What does
check(mid)mean? - What is the goal (min valid, max valid, exact match)?
- This will alter the return
- When is mid good/bad? Adjust left/right accordingly
- This will alter our
left =andright =updates
- This will alter our
- Do you return left, right, or mid?
Duplicates
If an input array has duplicates, then you need to tweak the check() function to try and find the first or last position of the desired target
If you have arr = [3, 4, 5, 5, 6, 7]
left = 0right = 5mid = 2, therefore,midpoints to the leftmost 5
Need to now change check() to use arr[mid] >= target - If we want to find the left most value, i.e. the "first occurrence", and we find a mid that matches our target, what do we need to do? We need to move our search space to maximum mid, and keep searching the leftern side for move values - i.e. right = mid
def binary_search(arr, target):
left = 0
right = len(arr)
while left < right:
mid = (left + right) // 2
if check(mid, arr, target):
right = mid
else:
left = mid + 1
return left
def check(idx, arr, target):
return(
arr[idx] >= target
)
Using len(arr) means your right boundary is past the last valid index, and your valid search interval is [left, right). In this you check left < right
Insertion vs Index
If we are looking to find the insertion index, there's a slight tweak versus finding a specific index and it mostly comes down to how you alter the check() function...as usual...and then the pointer that's returned
A very easy way to do this in python is via the bisect.bisect_left(arr, target) method - the below problem statement and python code shows it:
"Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order. You must write an algorithm with O(log n) runtime complexity."
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
return(bisect.bisect_left(nums, target))
- The
bisect_left(a, x, ...)function takes a sorted list a and a value x and returns an index i such that:- All elements to the left of the index (
a[:i]) are less than x - All elements to the right of and at the index (
a[i:]) are greater than or equal to x
- All elements to the left of the index (
Looking at the bisect_left source code, it's exactly our template, except with many more error handling and good coding practices
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums)
while left < right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
else:
right = mid
return(left)
bisect_righton the other hand will return an index i such that:- All elements to the left of the index (
a[:i]) are less than or equal to x - All elements to the right of the index (
a[:i]) are greater than x
- All elements to the left of the index (
The Longest Subsequence With Prefix Sum Problem utilizes bisect_right to find the length of the longest subsequence that's less than or equal to a certain query
- After calculating the prefix sum, the length of longest subsequence is equal to the last index of the prefix sum where we could insert the query
- If the pfx sum has
[1, 4, 7, 8], and our query is 6 or 7, we'd want to return 2
So the main difference is where it would return an index based on where values are equal
bisect_leftfinds the first occurrence of an item, or where it should be placed if there are none- "All elements to the left of
a[:i]are less than x"
- "All elements to the left of
bisect_rightfinds the last occurrence of an item, or where it should be placed if there are none- "All elements to the right of
a[:i]are greater than x"
- "All elements to the right of
- So they mostly differ on how they handle equal to, and exact insertion point
- If there was an array
arr = [1, 5, 6, 8]bisect_left(arr, 7)would return 3 as the 2nd index has a value less than it's targetbisect_left(arr, 6)would return 2 as it's the target, so less than or equal tobisect_right(arr, 7)would return 3 as the 2nd index has a value less than it's targetbisect_right(arr, 6)would return 3 as all elements to the left must be less than or equal to 6
Solution Spaces
Binary Search can also be used outside of arrays - generically it can be used on any solution space such as integers, some capacity, or anything else. A typical scenario of this is a problem asking "what is the min/max something can be done"
Ultimately, the only true criteria that need to be met for binary search are:
- You can quickly, in or better time, verify if the task if possible for a given input
x - If the task if possible for an input
x, and you are looking for:- A maximum, then it's also possible for all inputs less than
x - A minimum, then it's also possible for all inputs greater than
x
- A maximum, then it's also possible for all inputs less than
- If the task is not possible for an input
x, and you are looking for:- A maximum, then it's also impossible for all inputs greater than
x - A minimum, then it's also impossible for all inputs less than
x
- A maximum, then it's also impossible for all inputs greater than
Statement 1. references the ability to quickly do things, as the check() function needs to be fast enough that we can do better than , and statements 2. and 3. revolve around the search space being able to be "shrunk" via mid updates - if we can't shrink the search space automatically because something's unsorted, or it doesn't make sense, then we cannot do binary search (i.e. we can't cut out that portion of solution space)

Problems finding a min / max are actually searching for this magic threshold that separates possible from impossible, and that magic threshold is what we're trying to obtain as our output of binary search
Establishing the solution space is typically the hardest part - if you're looking for a min/max rate, how can you decide what "max" is?
- In Koko Eating Bananas Koko only eats a pile at a time maximum, and so the maximum rate can only be the maximum of the piles
max(piles) - In Capacity Planning you can ship as many packages as possible with a specific rate, but the most weight you could process in a single day is the entire weight, so the maximum rate is
sum(weights)
The solution space can be defined by which represents the range of the solution space - sometimes it's , sometimes it's where , etc...
Once you have the figured out, the binary search time complexity becomes
- revolves around the time taken for a check function to run - typically a greedy function that could exhaust the entire input list
- revolves around traversing the search space, where for each traversal we need to run the
check()function
Pointer Updates
The entire intuition of when to do left < right, left <= right, return left, return right, right = mid and / or left = mid + 1 revolves around pointers, solution spaces, duplicates, etc and while there are plenty of resources on templates for each of them, typically templates suck and intuition is the best method
When returning minimums, you return left - why?
When returning maximums, you return right - the Find Divisor Problem is an example of that
When you want to check even if left = right you use left <= right - typically this is only used during exact matches, to find minimums or maximums you just do left < right - why?
When working with binary search, the heart of the algorithm is how you define your search space and how you update your pointers. The classic question is: do you return left or right? Do you use left < right or left <= right? The answer depends on what you’re searching for - minimums, maximums, or exact matches - and how you want to handle duplicates
Imagine you’re searching for the minimum value that satisfies a condition. As you narrow your search space, you want to make sure you never skip over a possible answer. This means, whenever your check function says “yes, this works,” you move your right pointer to mid, keeping mid in the search space. When the loop ends, left will be at the smallest index that works, so you return left
Some Exact Match
In this one, we want to find something somewhere in an array, and the target must exist for us to return the index, otherwise you return insertion point
def binary_search(arr, target):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
# do something
return
if arr[mid] > target:
right = mid - 1
else:
left = mid + 1
# target is not in arr, but left is at the insertion point
return left
Example 1: Even Number of Elements
Array: [2, 4, 6, 8, 10, 12]
Target: 8
| Step | left | right | mid | arr[mid] | Comparison | Action |
|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 2 | 6 | 6 < 8 | left = mid + 1 (=3) |
| 2 | 3 | 5 | 4 | 10 | 10 > 8 | right = mid - 1 (=3) |
| 3 | 3 | 3 | 3 | 8 | 8 == 8 | return mid (=3) |
Example 2: Odd Number of Elements
Array: [1, 3, 5, 7, 9]
Target: 5
| Step | left | right | mid | arr[mid] | Comparison | Action |
|---|---|---|---|---|---|---|
| 1 | 0 | 4 | 2 | 5 | 5 == 5 | return mid (=2) |
Example 3: Insertion Point
Suppose the array is [2, 4, 6, 8, 10, 12] and the target is 7 (which does not exist in the array)
| Step | left | right | mid | arr[mid] | Comparison | Action |
|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 2 | 6 | 6 < 7 | left = mid + 1 (=3) |
| 2 | 3 | 5 | 4 | 10 | 10 > 7 | right = mid - 1 (=3) |
| 3 | 3 | 3 | 3 | 8 | 8 > 7 | right = mid - 1 (=2) |
At this point, left = 3 and right = 2, so the loop ends. The function returns left = 3, which is the index where 7 would be inserted to keep the array sorted. This matches the behavior of bisect_left([2, 4, 6, 8, 10, 12], 7), which also returns 3.
The below is very repetitive, but it is true The proof of why this is an insertion point is :
- Imagine if
arr[mid] < target- We know all
arr[:mid]are also< target - So we update
left = mid + 1
- We know all
- If
arr[mid] > target, then all elements at indices>= midare also> targetright = mid - 1
- If we're at some
midsuch thatleft > right, then we will know that- All elements to the left of
leftare< target - All elements to right of
leftare> target - At some point
left = mid + 1, orleft = 0- If it was ever updated to
mid + 1, that means we know at some pointarr[mid] < target - Therefore, the update it made is at some index where everything to the left of it is
< target [1, 3, 5, 8, 9], if the target is7, the firstmidindex would be0 + 5 // 2 = 2, and5 < 7soleft = 3. At this point every check will be between on numbers where the minimum range starts at index 3 which is 8- Left will never be updated again, right will continually scrunch down until it's less
- If it was ever updated to
- All elements to the left of
- Therefore, the reason left is the insertion point is the only way
leftis ever updated, is if we're sure everythingarr[:mid]at some point is always less than it, and then we place left pointer one before. If it's the insertion point, we'll never find an answer and it'll just stay there forever
Minimize
In this scenario it all comes down to Minimize k such that condition(k) is True
The reason we set right = mid is that we are looking to minimize k, and at any point if a condition is actually met, that just means we know it's included in the search space. k might be the actual min, and so we can't do right = mid - 1 like we did above
The reason right = mid - 1 worked above is that if the condition arr[mid] == target wasn't true, and arr[mid] > target, we knew for a fact that mid wasn't in the search space. mid - 1 might be, but mid for sure wasn't. In the minimize situation, if condition(k) is True, then k still may be in the search space
left starts as the minimum of the search space (maybe 0 for array indexes), if we ever make an update to left = mid + 1, that means that the condition(mid) failed, and we know for sure that mid is outside of the search space and can't possibly be a minimum candidate
left = 0, and that's the minleftwas updated tomid + 1, andmidfor sure wasn't an answer, soleft(which ismid + 1) is now the current min of the search space- It may never be updated again, and then it's the same as the first point
How do we know left is the minimum k that satisfies the condition? I always get caught up with "what if nothing in the search space satisfies the condition" for things like exact matches, but returning left at the end means we return insertion point of where it should be
- We setup search space to ensure any answer satisfies a condition
- If
leftis never upadted, it must be the min of the search space, so it's definitely the min that satisfies the condition! - If
leftwas updated, same logic as stated above - If we truly need an exact match, and we end up with
leftbutarr[left] != targetwe should return-1and notleft
while left < right:
mid = (left + right) // 2
if condition(mid): # go left to mid
right = mid
else: # go right
left = mid + 1
return left
Another point to mention here is setting right = len(arr) - there's a chance that target is greater than every single number in the arr. In that scenario we would continuously update left = mid + 1, and at some point either left = right = len(arr), or left = len(arr) - 1:
- If
left = right = len(arr), then returningleftis fine as we'd return 5 for the below array[0, 1, 2, 3, 4]- The insertion point of this array truly is
idx = 5, but thatidxjust doesn't exist
- If
left = len(arr) - 1, thenleft < rightstillmid = left + (right - left) // 2len(arr) - 1 + (len(arr) - (len(arr) - 1)) // 22 * len(arr) // 2 = len(arr)somid = len(arr) = right- At this point
arr[mid]would have anArrayIndexOutOfBoundserrorleft = len(arr) - 1right = len(arr) = midcheck(mid)would fail
- Nevermind, I'm wrong about portion 2.
- Weirdly enough
leftwill never becomelen(arr) - 1in either even or odd situation here - at some pointmidalways becomeslen(arr) - 1, and so whenleftupdates it becomesleft = right = len(arr)and so the loop returns - Intuition on why scenario 2 never happens during an open interval (
right = len(arr), left < right) binary search:- I screwed up the order of operations -
(right - low) // 2would be evaluated before being added tolow len(arr) - (len(arr) - 1) // 21 // 2which would truncate to 0, somid = len(arr) - 1
- I screwed up the order of operations -
- TODO: Update section 2 above and re-explain all this crap... f bsearch it's so stupid why didn't I just take notes in college
- Weirdly enough
Example: Find First Element Target
Array: [1, 3, 5, 7, 9, 11]
Target: 6
Goal: Find the first index where arr[i] 6
| Step | left | right | mid | arr[mid] | arr[mid] 6? | Action |
|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 2 | 5 | No | left = mid + 1 (=3) |
| 2 | 3 | 5 | 4 | 9 | Yes | right = mid (=4) |
| 3 | 3 | 4 | 3 | 7 | Yes | right = mid (=3) |
| 4 | 3 | 3 | - | - | - | End, return left=3 |
Result: Returns index 3 (arr[3]=7), which is the first element 6.
Edge Case: All Elements Less Than Target
Array: [1, 2, 3, 4, 5]
Target: 10
Goal: Find the first index where arr[i] 10
| Step | left | right | mid | arr[mid] | arr[mid] 10? | Action |
|---|---|---|---|---|---|---|
| 1 | 0 | 4 | 2 | 3 | No | left = mid + 1 (=3) |
| 2 | 3 | 4 | 3 | 4 | No | left = mid + 1 (=4) |
| 3 | 4 | 4 | 4 | 5 | No | left = mid + 1 (=5) |
| 4 | 5 | 4 | - | - | - | End, return left=5 |
Result: Returns index 5 (out of bounds), meaning no element 10 exists.
Edge Case: First Element Satisfies Condition
Array: [2, 3, 4, 5, 6]
Target: 2
Goal: Find the first index where arr[i] 2
| Step | left | right | mid | arr[mid] | arr[mid] 2? | Action |
|---|---|---|---|---|---|---|
| 1 | 0 | 4 | 2 | 4 | Yes | right = mid (=2) |
| 2 | 0 | 2 | 1 | 3 | Yes | right = mid (=1) |
| 3 | 0 | 1 | 0 | 2 | Yes | right = mid (=0) |
| 4 | 0 | 0 | - | - | - | End, return left=0 |
Result: Returns index 0 (arr[0]=2), which is the first element 2.
Upper Bound (Last Valid X)
This is the flip scenario of Lower Bound, and so in this scenario you set left = mid and right = mid - 1
This is because there can be multiple mid that satisfy the result, but you want to find the last one so you keep shrinking / dragging search space to the right
mid calculation being left + right + 1 also prevents an infinite loop, and is vital
while left < right:
mid = (left + right + 1) // 2 # Bias right
if condition(mid): # go right
left = mid
else: # go left
right = mid - 1
return left
Search On Answer
Search On Answer problems usually mean changing the search space, and then finding the Lower Bound or Upper Bound based on problem statement
left = max(weights)
right = sum(weights)
while left < right:
mid = (left + right) // 2
if can_ship_in_days(mid):
right = mid
else:
left = mid + 1
return left
ATypical
There are some weird ones thrown in as well, especially rotating lists, a weird search space, or "guessing" at a condition
Rotating Lists
Problem Statement:
Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:
[4,5,6,7,0,1,2] if it was rotated 4 times.
[0,1,2,4,5,6,7] if it was rotated 7 times.
Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]]
In these scenarios, the condition(mid) function needs to change to figure out if you should go left or right
If an array isn't sorted, then you know for sure last element at end first element at 0
However, if an array is rotated, then the last element would be smaller than the first element - seeing this pattern you can realize there's a place, an Inflection Point where you can figure out where the real start was
Therefore, what you need to search for is an index which would correspond to the old start and end
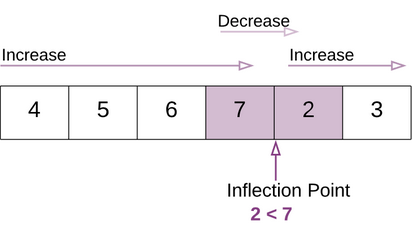
Therefore, check becomes:
mid = left + right // 2
if check(mid):
return(mid)
elif mid > first element of array:
search to the right
else:
search to the left
because if you find the number 6, which is above the first element 4, you know our inflection point is still to the right of us
Find A Rate
There are some specific problems like KoKo Eating Bananas and Elves on Package Line where you basically need to find a rate of something, and then check if that rate suffices
Koko's eating rate, maybe it's 3 bananas-per-hour, and if that works then we'd look if a higher rate would suffice like 10-per-hour, etc...
Usually this would mean the rate finding is where is the rate search space, and then there'd be an input array of size that you must check through. The check function is typically so in total it's versus
Otherwise, you just continuously check the rate instead of "smart searching" using binary search
Structures
Lists and Tree's are typically the data structures that you see with Binary Search
Lists
There's some gotchas for list, mostly around defining right and left, and different vs , but altogether the pseudocode is pretty easy Pseudocode for list:
# list of 10 nums
nums = sorted(list)
val_to_find = get_num()
left = 0
right = len(nums)
while left <= right:
# 0 + (10 - 0) // 2 = 5 // 2 = 2
mid = left + (right - left) // 2
if check(val):
left = mid + 1 # or left = mid
else:
right = mid - 1 # or right = mid
return(-1)
Tree
In a binary search tree, there's some special properties where, for any Vertex V, it's right child is greater than it's value, and its left child is less than it's value
Ultimately it's just a way to restructure a Linked List so that search is in time - this entire concept is the idea of Self-Balancing Binary Search Trees such as B-Tree's. Self balancing tree's have less efficient writes (since they need to find where to place nodes and do some restructuring), but the idea is that reads are much more efficient
A Binary Search Tree has similar code structure to Lists
def search_bst(root, target):
while root is not None:
if root.val == target:
return True
elif target < root.val:
root = root.left
else:
root = root.right
return False